PUBLICATIONS

2025

1. arXiv

   

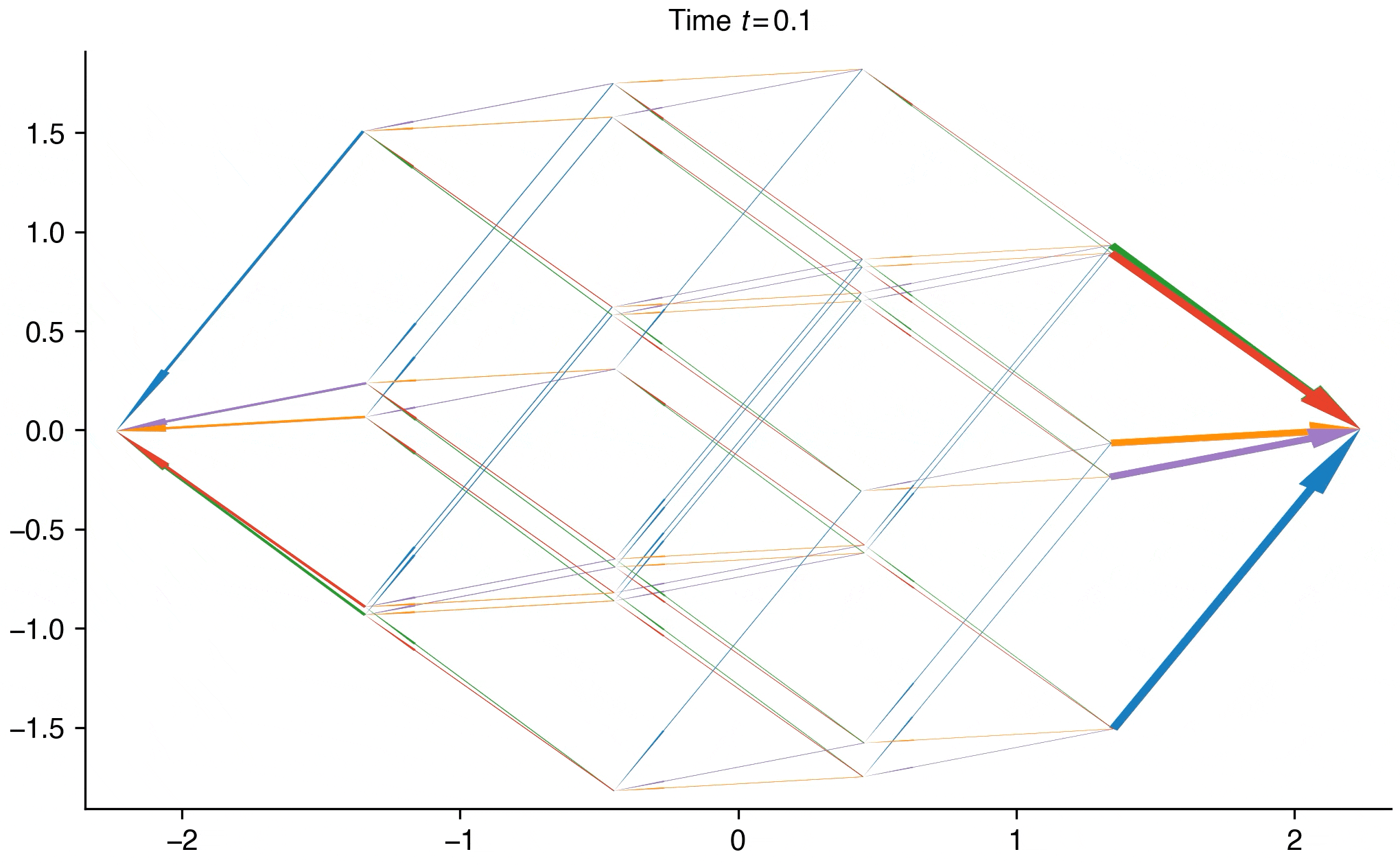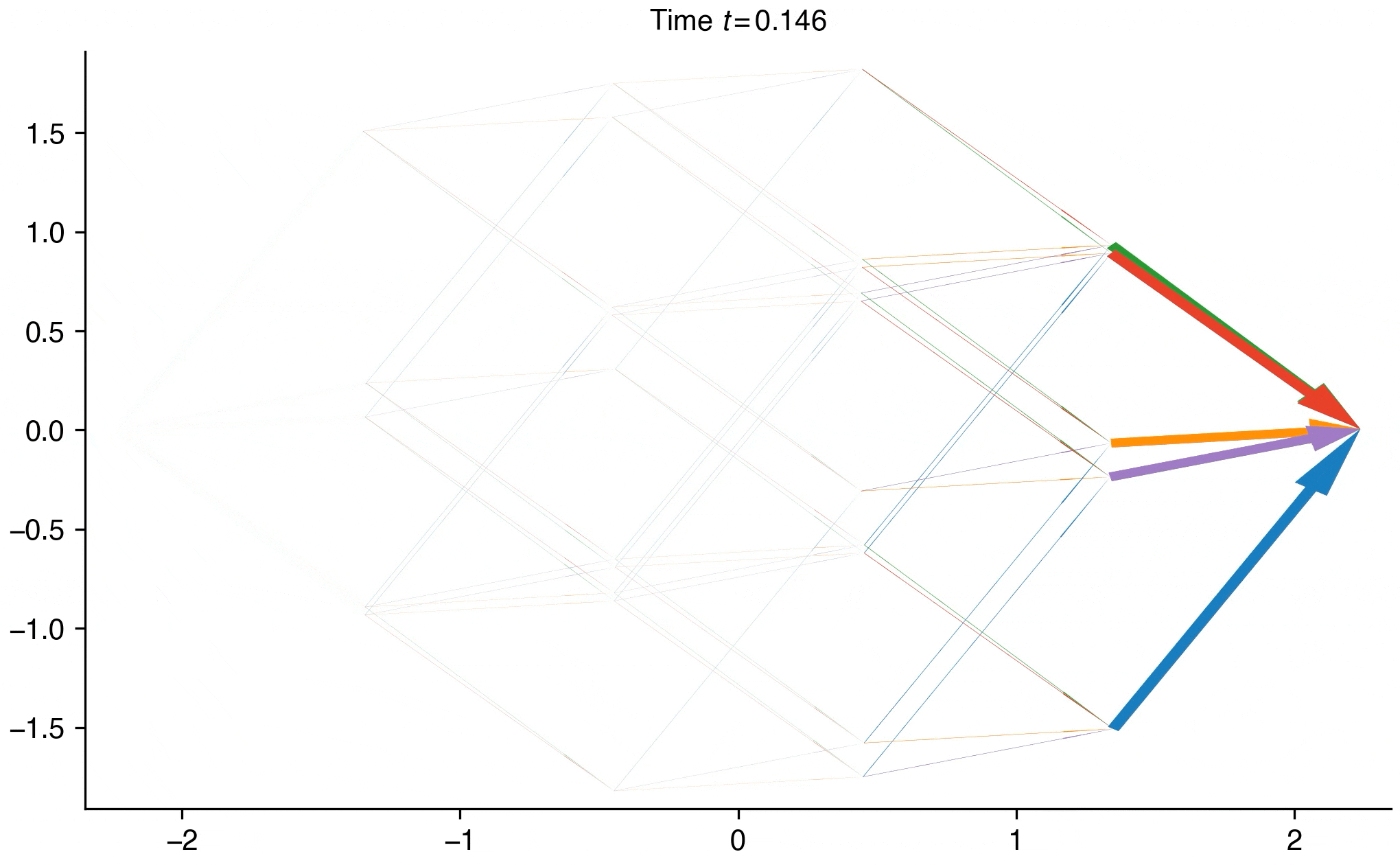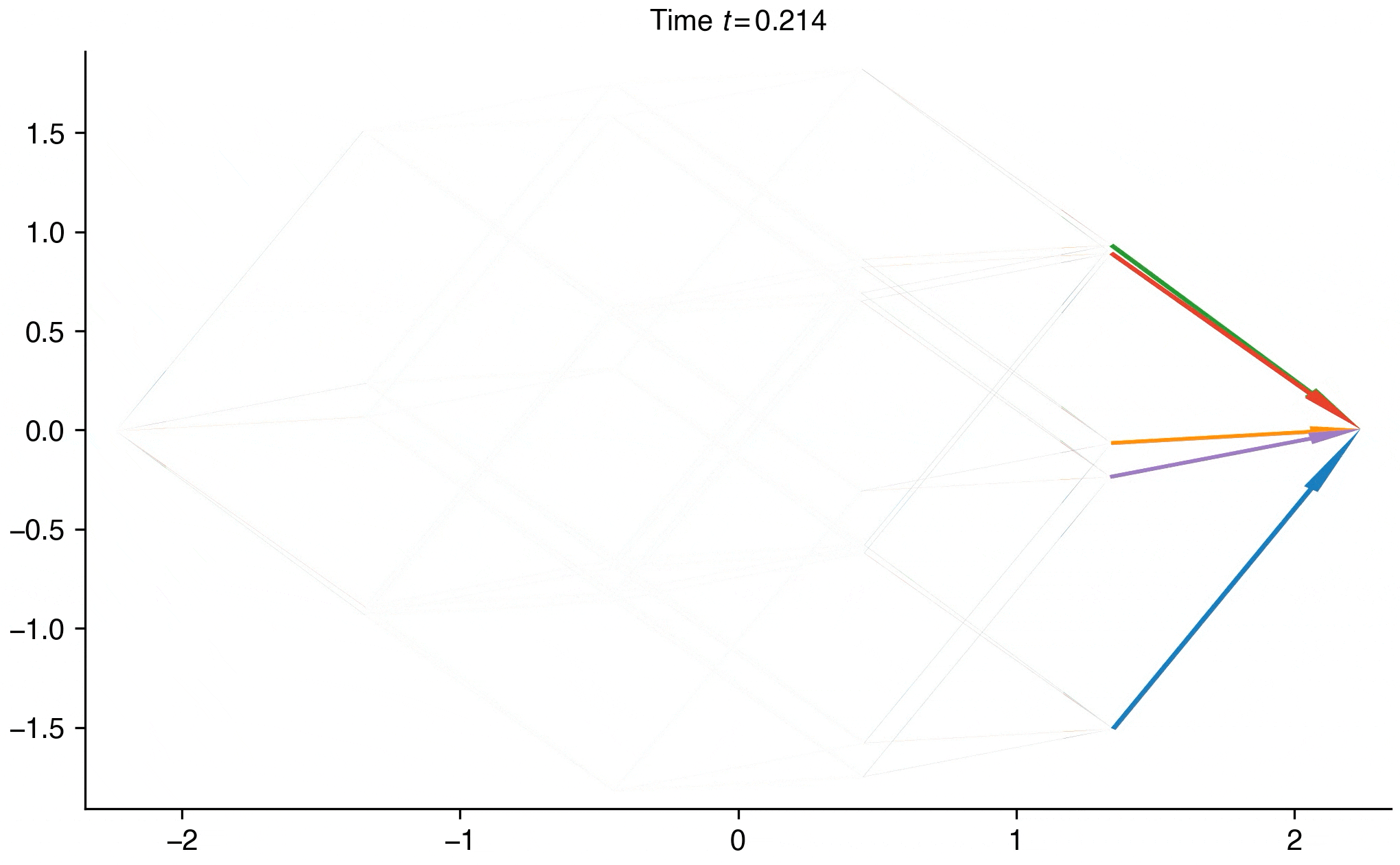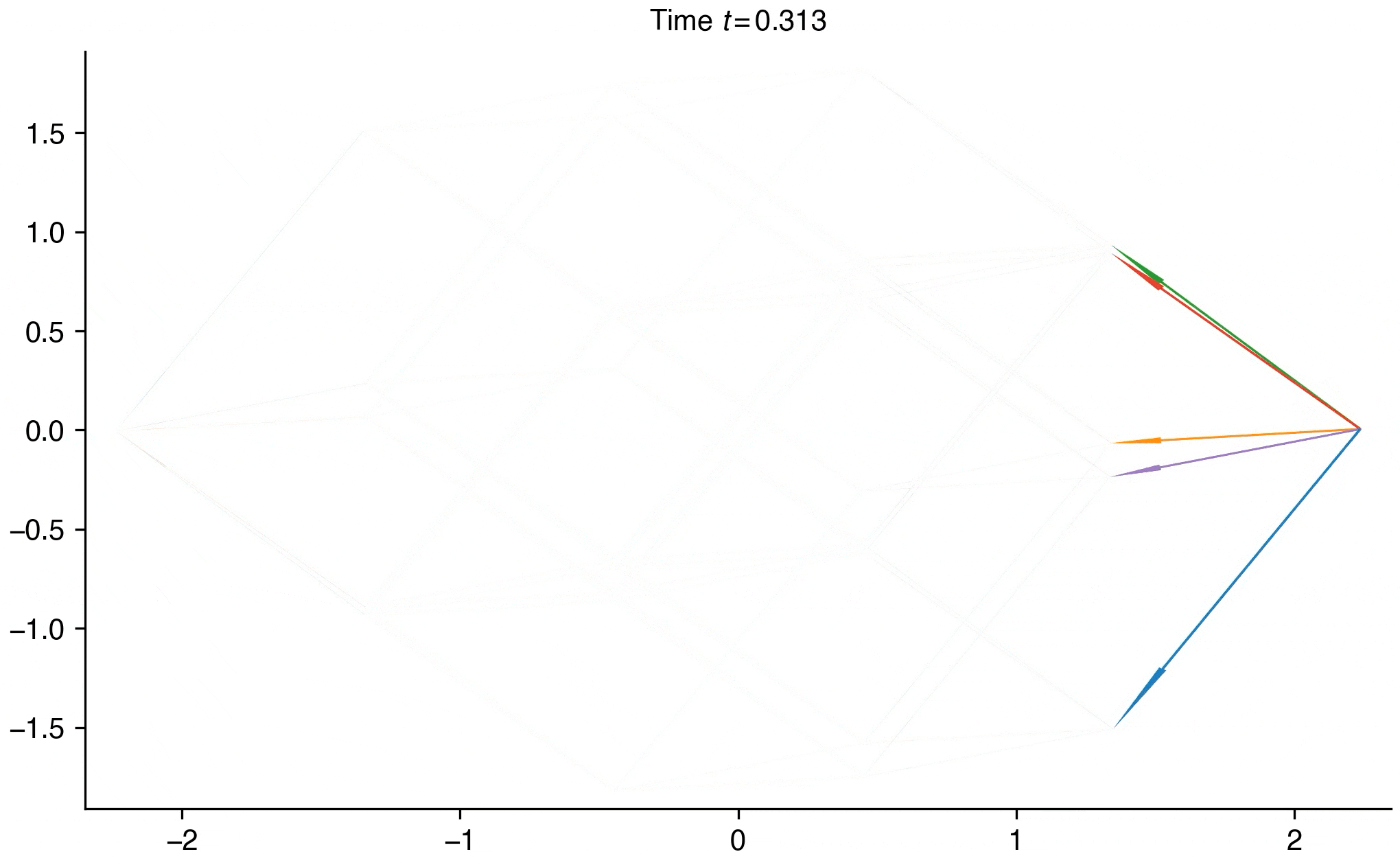
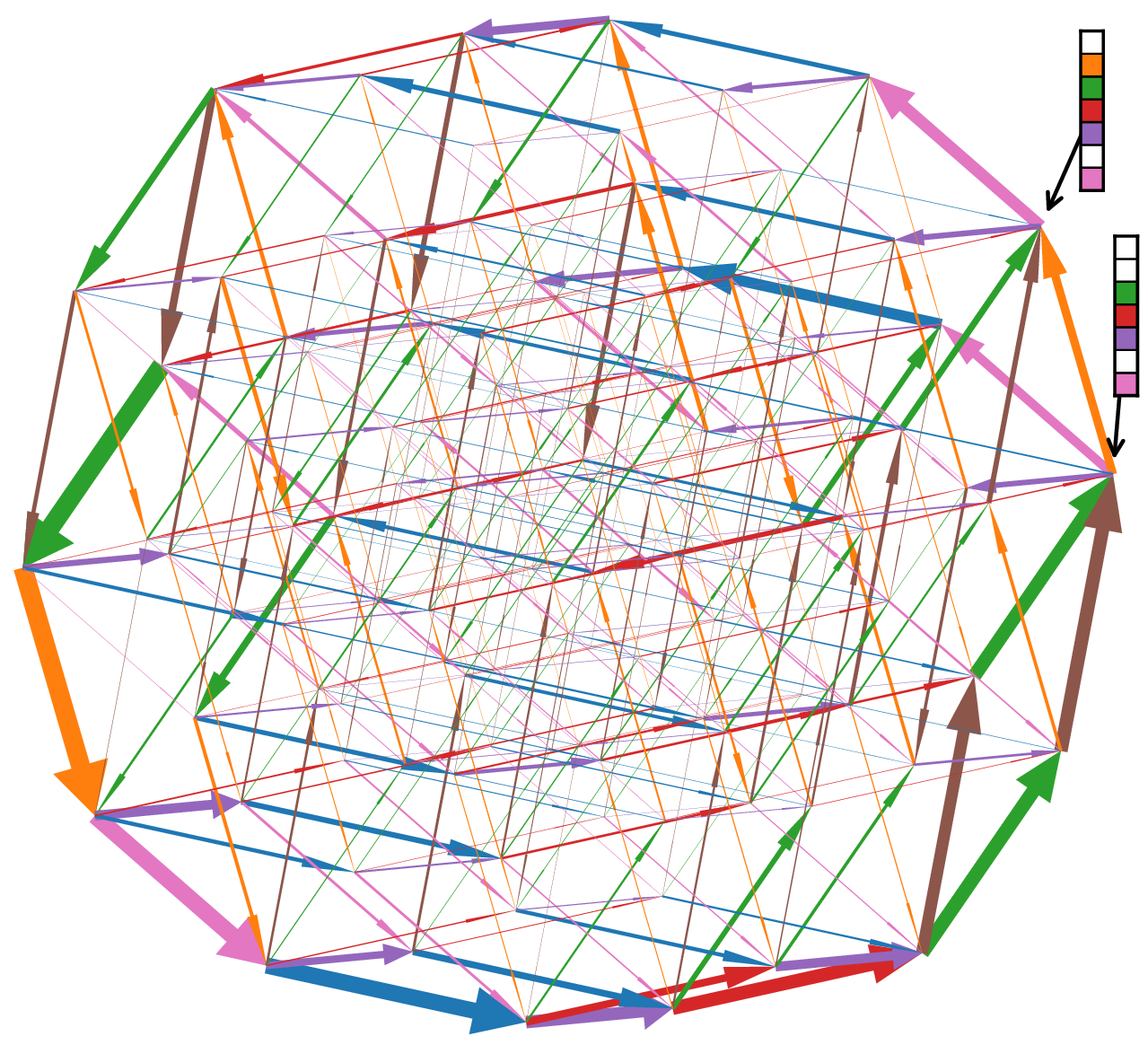
   Distinguishing thermal versus quantum annealing using probability-flux signatures across interaction networks

   Yoshiaki Horiike and Yuki Kawaguchi

   arXiv preprint, Nov 2025

   Abs arXiv Poster

   Simulated annealing provides a heuristic solution to combinatorial optimization problems. The cost function of a problem is mapped to the energy function of a physical many-body system, and, using thermal or quantum fluctuations, the system explores the state space to find the ground state, which may correspond to the optimal solution of the problem. Studies have highlighted both the similarities and differences between thermal and quantum fluctuations. Nevertheless, fundamental understanding of thermal and quantum annealing remains incomplete, making it difficult to design problem instances that fairly compare the two methods. Here, we investigate the many-body dynamics of thermal and quantum annealing by examining all possible interaction networks of ±J Ising spin systems up to seven spins. Our comprehensive investigation reveals that differences between thermal and quantum annealing emerge for particular interaction networks, indicating that the structure of the energy landscape distinguishes the two dynamics. We identify the microscopic origin of these differences through probability fluxes in state space, finding that the two dynamics are broadly similar but that quantum tunnelling produces qualitative differences. Our results provide insight into how thermal and quantum fluctuations navigate a system toward the ground state in simulated annealing, and are experimentally verifiable in atomic, molecular, and optical systems. Furthermore, these insights may improve mappings of optimization problems to Ising spin systems, yielding more accurate solutions in faster simulated annealing and thus benefiting real-world applications in industry. Our comprehensive survey of interaction networks and visualization of probability flux can help to understand, predict, and control quantum advantage in quantum annealing.

2. arXiv

   

   Distinct weak asymmetric interactions shape human brain functions as probability fluxes

   Yoshiaki Horiike and Shin Fujishiro

   arXiv preprint, Aug 2025

   Abs arXiv Slides

   The functional computation of the human brain arises from the collective behaviour of the underlying neural network. The emerging technology enables the recording of population activity in neurons, and the theory of neural networks is expected to explain and extract functional computations from the data. Thermodynamically, a large proportion of the whole-body energy is consumed by the brain, and functional computation of the human brain seems to involve high energy consumption. The human brain, however, does not increase its energy consumption with its function, and most of its energy consumption is not involved in specific brain function: how can the human brain perform its wide repertoire of functional computations without drastically changing its energy consumption? Here, we present a mechanism to perform functional computation by subtle modification of the interaction network among the brain regions. We first show that, by analyzing the data of spontaneous and task-induced whole-cerebral-cortex activity, the probability fluxes, which are the microscopic irreversible measure of state transitions, exhibit unique patterns depending on the task being performed, indicating that the human brain function is a distinct sequence of the brain state transitions. We then fit the parameters of Ising spin systems with asymmetric interactions, where we reveal that the symmetric interactions among the brain regions are strong and task-independent, but the antisymmetric interactions are subtle and task-dependent, and the inferred model reproduces most of the observed probability flux patterns. Our results indicate that the human brain performs its functional computation by subtly modifying the antisymmetric interaction among the brain regions, which might be possible with a small amount of energy.

3. arXiv

   

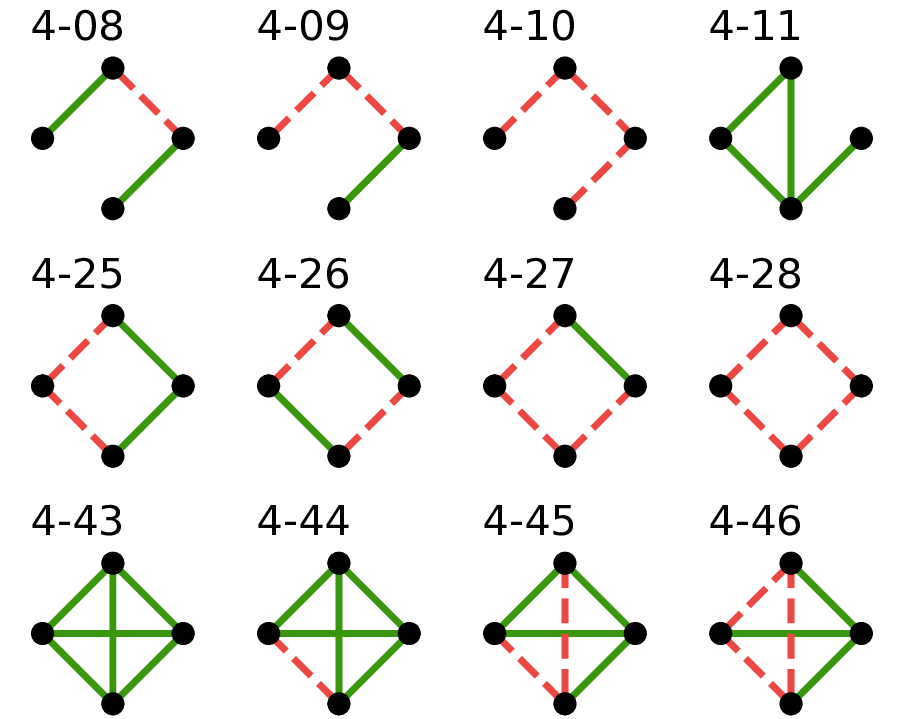
   A comprehensive exploration of interaction networks reveals a connection between entanglement and network structure

   Yoshiaki Horiike and Yuki Kawaguchi

   arXiv preprint, May 2025

   Abs arXiv Poster Slides

   Quantum many-body systems are typically studied assuming translational symmetry in the interaction network. Recent experimental advances in various platforms for quantum simulators have enabled the realization of irregular interaction networks, which are intractable to implement with conventional crystal lattices. Another hallmark of these advances is the ability to observe the time-dependent behaviour of quantum many-body systems. However, the relationship between irregular interaction networks and quantum many-body dynamics remains poorly understood. Here, we investigate the connection between the structure of the interaction network and the eigenstate entanglement of the quantum Ising model by exploring all possible interaction networks up to seven spins. We find that the eigenstate entanglement depends on the structure of the Hilbert space diagram, particularly the structure of the equienergy subgraph. We further reveal a correlation linking the structure of the Hilbert space diagram to the number of unconstrained spin pairs. Our results demonstrate that the minimum eigenstate entanglement of the quantum Ising model is governed by the specific structure of the interaction network. We anticipate that our findings provide a starting point for exploring quantum many-body systems with arbitrary interactions and finite system size. Moreover, our approach may be applicable to other quantum many-body systems, such as the Hubbard model.

4. Phys. Rev. E

   

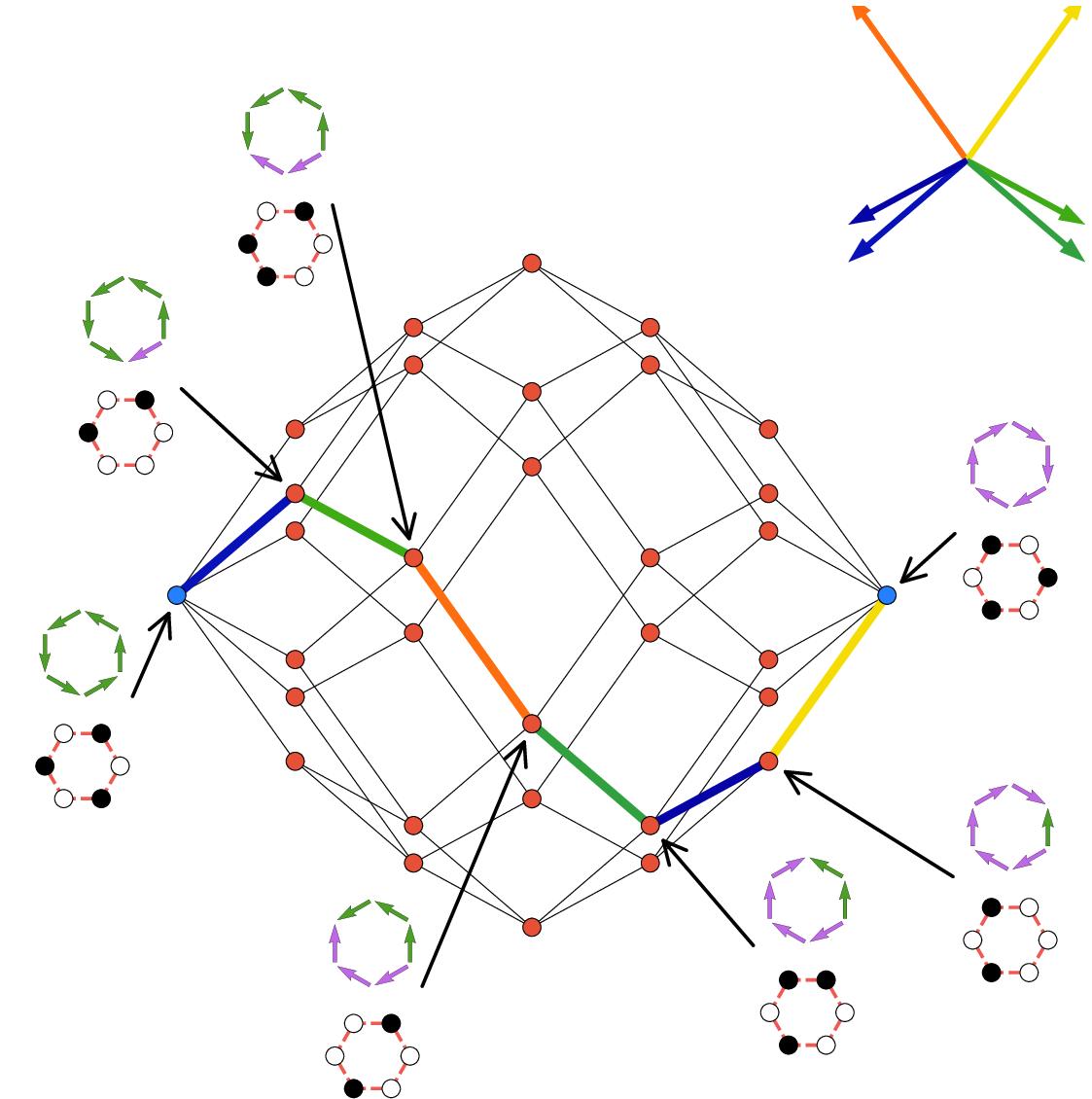
   Orthogonal projections of hypercubes

   Yoshiaki Horiike and Shin Fujishiro

   Physical Review E, Oct 2025

   Abs DOI arXiv HTML PDF Supp Code Poster Slides

   Projections of hypercubes have been applied to visualize high-dimensional binary state spaces in various scientific fields. Conventional methods for projecting hypercubes, however, face practical difficulties. Manual methods require nontrivial adjustments of the projection basis, while optimization-based algorithms limit the interpretability and reproducibility of the resulting plots. These limitations motivate us to explore theoretically analyzable projection algorithms such as principal component analysis (PCA). Here, we investigate the mathematical properties of PCA-projected hypercubes. Our numerical and analytical results show that PCA effectively captures polarized distributions within the hypercubic state space. This property enables the assessment of the asymptotic distribution of projected vertices and error bounds, which characterize the performance of PCA in the projected space. We demonstrate the application of PCA to visualize the hypercubic energy landscapes of Ising spin systems, specifically finite artificial spin-ice systems, including those with geometric frustration. By adding projected hypercubic edges, these visualizations reveal pathways of correlated spin flips. We confirm that the time-integrated probability flux exhibits patterns consistent with the pathways identified in the projected hypercubic energy landscapes. Using the mean-field model, we show that dominant state transition pathways tend to emerge around the periphery of the projected hypercubes. Our work provides a better understanding of how PCA discovers hidden patterns in high-dimensional binary data.

5. Phys. Rev. E

   

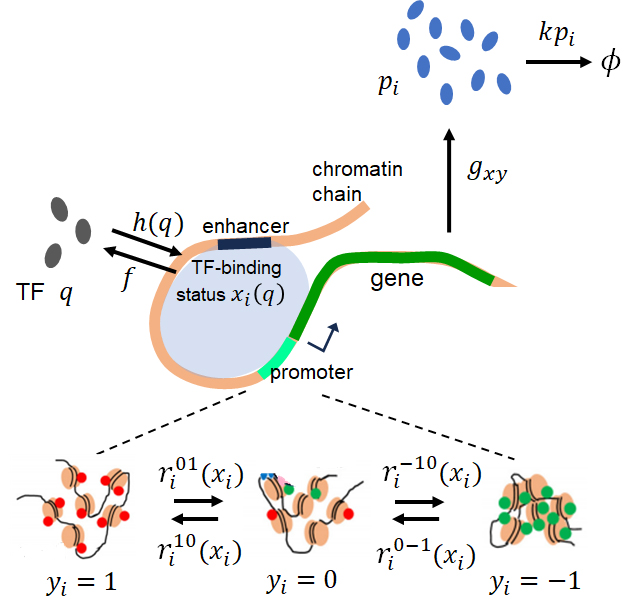
   Landscapes and nonequilibrium fluctuations of eukaryotic gene regulation

   Masaki Sasai, Bhaswati Bhattacharyya, Shin Fujishiro, and 1 more author

   Physical Review E, Oct 2025

   Abs DOI arXiv HTML

   Understanding the interplay among processes that occur over different timescales is a challenging issue in the physics of systems regulation. In gene regulation, the timescales for changes in chromatin states can differ from those for changes in the concentration of product protein, raising questions about how to understand their coupled dynamics. In this study, we examine the effects of these different timescales on eukaryotic gene regulation using a stochastic model that describes the landscapes and probability currents of nonequilibrium fluctuations. This model shows that slow, nonadiabatic transitions of chromatin states significantly impact gene-regulation dynamics. The simulated circular flow of the probability currents indicates a maximum entropy production when the rates of chromatin-state transitions are low in the intensely nonadiabatic regime. In the mildly nonadiabatic regime, this circular flow fosters hysteresis, suggesting that changes in chromatin states precede changes in transcription activity. Furthermore, calculations using a model of a circuit involving three core genes in mouse embryonic stem cells illustrate how the timescale difference can tune fluctuations in individual genes. These findings highlight the rich effects of nonadiabatic chromatin-state transitions on gene regulation in eukaryotic cells.