Yoshiaki Horiike

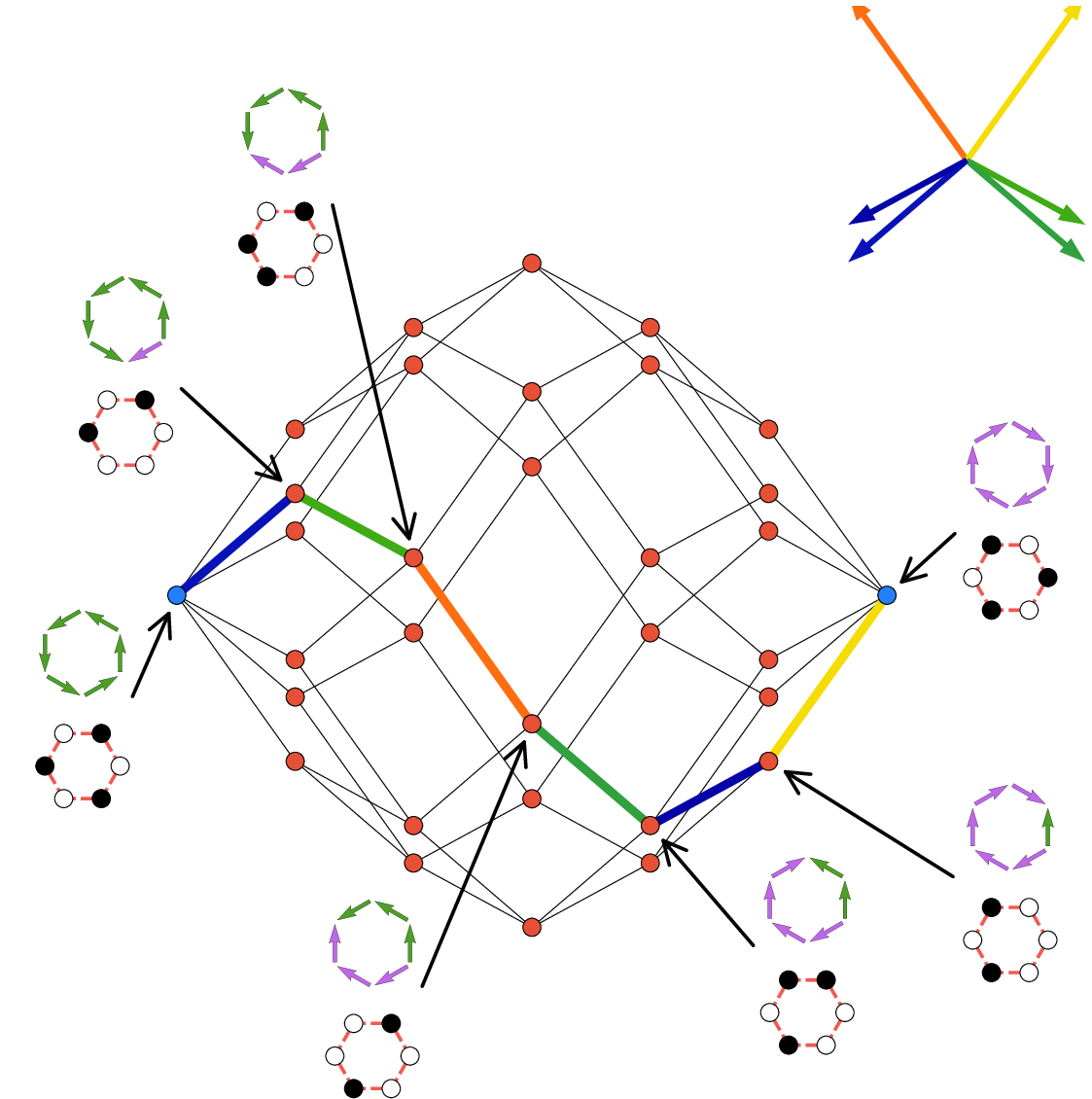
Projections of hypercubes have been applied to visualize high-dimensional binary state spaces in various scientific fields. Conventional methods for projecting hypercubes, however, face practical difficulties. Manual methods require nontrivial adjustments of the projection basis, while optimization-based algorithms limit the interpretability and reproducibility of the resulting plots. These limitations motivate us to explore theoretically analyzable projection algorithms such as principal component analysis (PCA). Here, we investigate the mathematical properties of PCA-projected hypercubes. Our numerical and analytical results show that PCA effectively captures polarized distributions within the hypercubic state space. This property enables the assessment of the asymptotic distribution of projected vertices and error bounds, which characterize the performance of PCA in the projected space. We demonstrate the application of PCA to visualize the hypercubic energy landscapes of Ising spin systems, specifically finite artificial spin-ice systems, including those with geometric frustration. By adding projected hypercubic edges, these visualizations reveal pathways of correlated spin flips. We confirm that the time-integrated probability flux exhibits patterns consistent with the pathways identified in the projected hypercubic energy landscapes. Using the mean-field model, we show that dominant state transition pathways tend to emerge around the periphery of the projected hypercubes. Our work provides a better understanding of how PCA discovers hidden patterns in high-dimensional binary data.